Multi-Language for Visual Studio
Quick Tour (Windows Store Apps)
Activating the Multi-Language Add-In
After you have installed the Add-In, there will be a new menu item in the Tools menu in Visual Studio.
This menu item activates the Add-In and shows it in a tool-window. You can dock this window at the side of the main Visual Studio window, or drag it into a tab group, like other tool windows in Visual Studio. It's probably best to place it at the bottom, in a wide format.
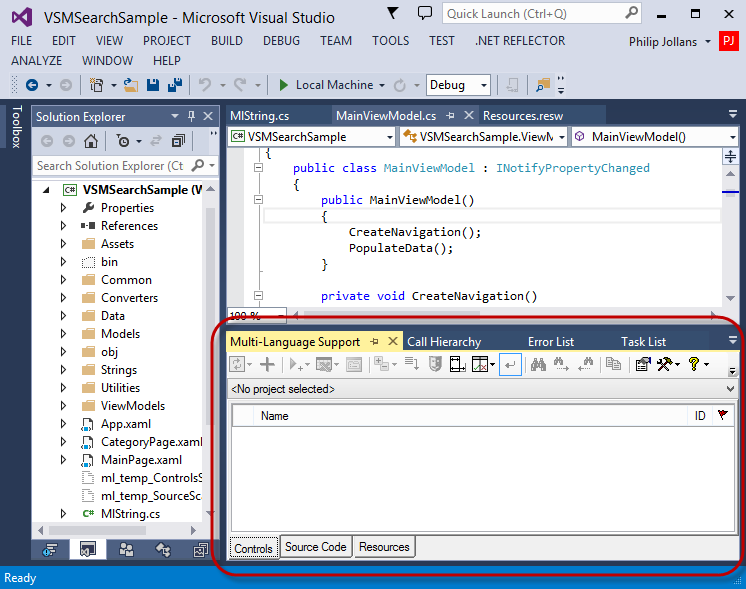
Selecting a project
A Visual Studio solution may contain multiple projects. The Multi-Language Add-In usually works with a single project. To get started, you must first select the project. There are two ways to do this.
| from a dialog | When you select the Add-In from the tools menu, it will probably show a list of the projects in a dialog. Simply select the project and click on OK. 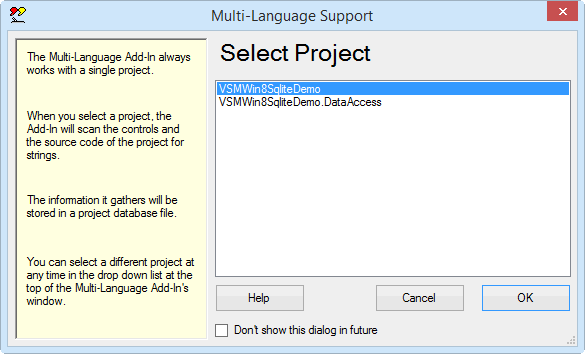
This dialog can be disabled, so if somebody else has already worked with the Add-In, it might not appear. |
| from a drop down list | At the top of the Add-In's main window, just below the toolbar, there is a drop down project list 
You can select a different project at any time from this list. |
Initialising the project for localization
When you select a Windows Store project, the Add-In will automatically detect:
|

|
|

|

|
This dialog will probably be followed by second dialog, with options for scanning the project. Just click on OK to accept the default options. |
| <project name>_ml.xml | This is the project database used by the Add-In. It is added to the project with BuildAction=None. |
| mlstring.vb or mlstring.cs | This module contains support functions, in particular the function ml.GetString(), which is used to load localized strings. |
Scanning the project
The Add-In will now scan the project. This is performed in three phases:
| Resource files | String resources defined for the default language in a resource file with the .resw extension are read and displayed in the Resources tab. |
| Controls | The user interface definition in the XAML files is read. Texts which can be translated are displayed in the Controls tab. |
| Source code | The project source code is scanned for texts which may require translation. The texts are displayed ih the Source code tab. |

|
The results of the scan are displayed in three separate grids in the Add-In's window. You can switch between these grids using the tabs at the bottom of the window. |
Adding a second language
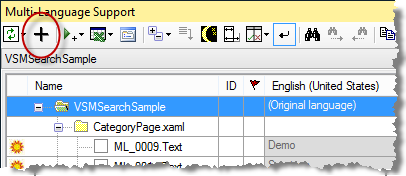
To add a new language to the project, click on the  symbol on the Add-In's toolbar.
symbol on the Add-In's toolbar. |
|
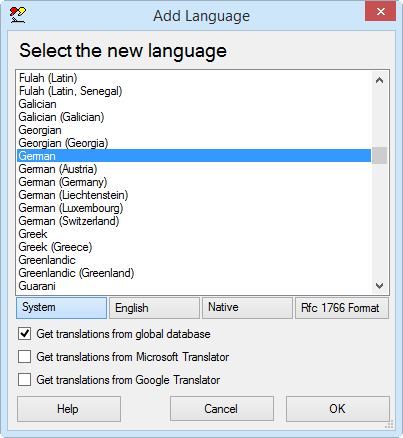
|
Select a new language from the list. The buttons below the list change the way the list is displayed. In particular, the button English simply shows the language names in English. It does not select English in the list. If the Microsoft Translator supports both the default language and the selected language then the option Get translations from Microsoft Translator is enabled. Similarly for the Google Translator. Select one of these options if you want the texts to be translated automatically using an online service. Click on OK to add this language to the project. |
Some languages, such as German or French, are considered to be neutral languages. The regional variations, such as German(Germany), German(Austria), French(France) or French(Canada) are referred to as specific languages. You should usually start with the neutral language.
After adding the second language, the Add-In will
- add a new column to the grids for the new language
- search for translations of common texts such as OK and Cancel in the Global Translations Database
- if you selected the Microsoft or Google Translator option, then it will translate all other texts using the online service
Now we will take a closer look at the three grids.
The controls grid
To see the controls grid, make sure that the controls tab at the bottom of the window is selected. The grid should look something like the following screenshot.
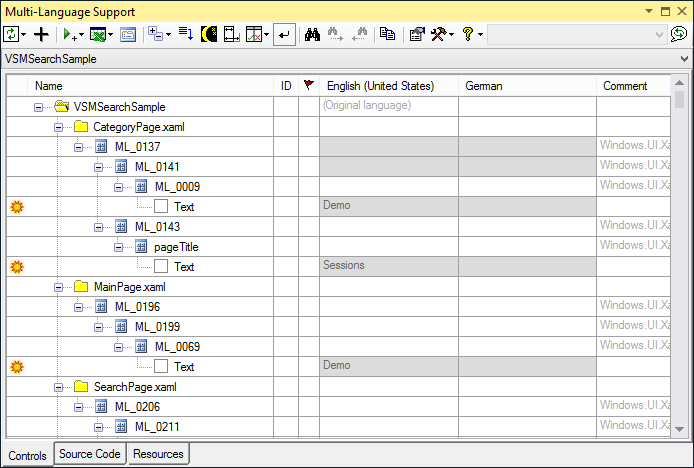
By default, the text attributes are shown in a hierarchical manner, showing the structure of the XAML file. As an alternative, you can view the text attributes for each XAML file in a flat list. To select this mode, click on the  button on the toolbar and then select Flat list from the menu, as shown below:
button on the toolbar and then select Flat list from the menu, as shown below:
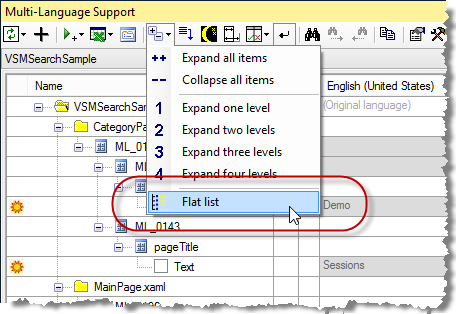
The controls grid will then look something like the following screenshot.

If an element in the XAML structure does not have a name, then it is assigned one by the Add-In. As you can see, these names have the form ML_0000 with 0000 is a numeric value.
To the left of each name of each text attribute there is a check box which indicates whether the attribute has been selected for translation. Initially, none of the attributes are selected. To select an attribute, simply click on the check box. Alternatively, you can select the line and hit the space bar.

As you can see, the grid has a column for each language in the project. Once a property has been selected, you can enter a translation simply by clicking on the cell in the appropriate column and entering the translation. If you are able to translate the text yourself, this is the easiest way enter translations.
If a text is shown in light grey, then it is the text which would be retrieved at runtime via the resource fallback mechanism. In general, if a text is not defined for a specific language (e.g. Spanish(Mexico)) then the text for the neutral language (e.g. Spanish) would be used. If this has not been defined, then the text for the default language would be used.
When you select a text attribute, the XAML code may be modified, so that the attribute is initialised from a resource file. The exact modification depends on several factors, as described below:
|
Text attribute of a XAML control |
The attribute x:Uid is added. A resource string is defined with the name <Uid>.<Attribute name> The Uid is always generated in the form ML_<numeric value>, because it must be unique in the complete project. Example Before <Button Content="OK" x:Name="OKButton" Click="OKButton_Click" /> Example After <Button Content="OK" x:Name="OKButton" Click="OKButton_Click" x:Uid="ML_0009" /> A resource string with the name ML_0009.Content is defined with the text "OK". |
|
A simple text in a TextBlock control |
A single text can be handled as a Text attribute, and localized with a resource with the name <Uid>.Text. Example Before <TextBlock>One</TextBlock> Example After <TextBlock x:Uid="ML_0011">One</TextBlock>> A resource string with the name ML_0011.Content is defined with the text "One". |
|
One of multiple texts in a TextBlock control |
If there is more than one text in a TextBlock, the text is replaces with s Run tag, which can be localized with the Text attribute. Example Before Here, the content of the TextBlock is broken by a LineBreak tag. <TextBlock>One<LineBreak/>Two</TextBlock> Example After <TextBlock><Run x:Uid="ML_0014">One</Run><LineBreak />Two</TextBlock> The text before the LineBreak is converted to a Run tag and assigned the Uid ML_0014. A resource string with the name ML_014.Text is defined with the text "One". |
|
Not all texts in the XAML file require translation. The screen shot on the right shows some texts which you might not want to translate. |

|

|
The best thing to do is to hide these texts. The first step is to click on the sun symbol  at the left hand margin.
at the left hand margin. The sun symbol is replaced by a moon symbol  .
.The second step is to click on the toggle button on the toolbar, which has either a moon symbol 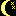 or a sunset symbol
or a sunset symbol  .
. |
The symbol on the toolbar is replaced by the sun symbol  and the hidden texts are actually hidden.
and the hidden texts are actually hidden.If you click on the button again, then the hidden texts are displayed once more. |

|
The best practice is to go through every text and either:
- select it for translation or
- hide it.
This makes it easier to maintain the localization in future versions of your application, because you can easily identify new texts in the project.
The source code grid
To see the source code grid, make sure that the source code tab at the bottom of the window is selected. The grid should look something like the following screenshot.
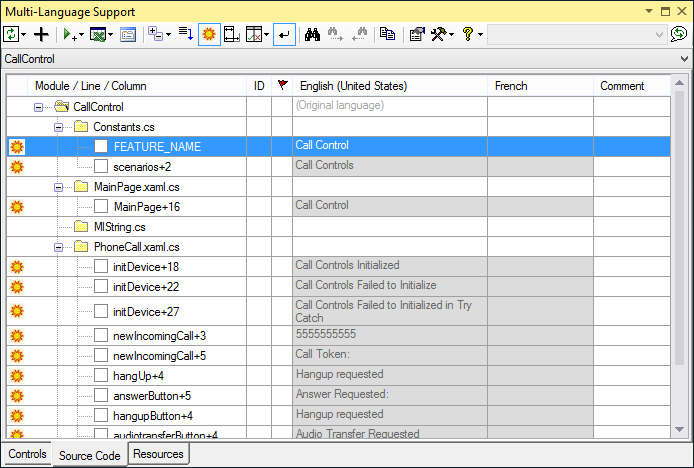
The left hand column shows the function name and the line number within that function. For example the text "Call controls initialized" is at line 18 in the function initDevice().
As in the controls grid:
- you can select a text for translation by clicking on the checkbox
 or
or
- hide the text by clicking on the sun symbol
 .
.
number.
When you click on a line in the source code grid, the corresponding line in the source code will be shown in the source editor.
If you click on a text in the source editor with the right (or secondary) mouse button, you can select the command "Show in Multi-Language" from the context menu, which will locate the text in the source code grid.
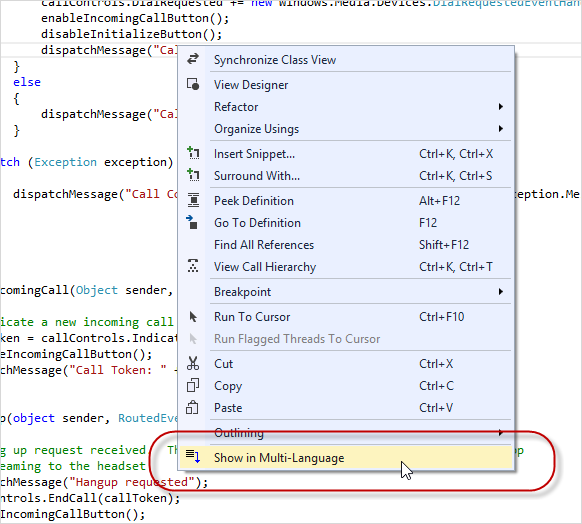
This is identical to placing the cursor on a string and clicking on the "Goto line" symbol  on the Add-In's toolbar.
on the Add-In's toolbar.
When you select a string for translation by clicking on the checkbox, the Add-In will generate a resource string (with a name based on the original text) and insert a call to the function ml.GetString() into the source code.

The function ml.GetString() is in the module mlstring.cs (or mlstring.vb) which has already been added to your project.
In this case, the text Call Control has been replaced with ml.GetString("Call_Control") and new resource string named "Call_Control" has been generated.
Once a string has been selected for translation, you can enter a translation simply by typing a new text into the grid.
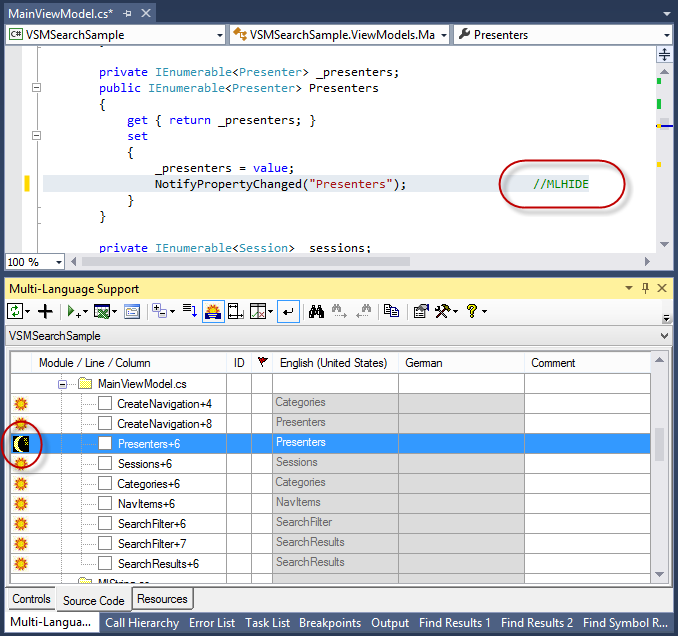
As with the controls grid, you also have the option of hiding texts which do not require translation. For example, the property name passed to the function NotifyPropertyChanged (in the screen shot below) must not be translated.
As before, we hide a string by clicking on the sun symbol  at the left hand margin, which is then replaced by a moon symbol
at the left hand margin, which is then replaced by a moon symbol  . At the same time, the comment //MLHIDE ('MLHIDE in VB.NET) is added to the end of the source code line, to mark it as hidden.
. At the same time, the comment //MLHIDE ('MLHIDE in VB.NET) is added to the end of the source code line, to mark it as hidden.
As with the controls grid, the texts are actually hidden after you click on the toggle button on the toolbar, with a moon  or a sunset
or a sunset  symbol, which is then replaced by a sun symbol
symbol, which is then replaced by a sun symbol  .
.
Once again, it is the best practice is to go through every text and either:
- select it for translation or
- hide it
because this makes it easier to maintain the localization in future versions of your application.
You can also add the MLHIDE comment to lines in the source code editor. When the Add-In scans the project, it will automatically hide these strings.
Filtering texts with regular expressions
In many cases, you will be able to select, or alternatively hide, texts in the source code based on simple rules. For example you will probably not want to translate SQL strings, or the parameters to an event logging function. On the other hand, you will probably always want to translate the parameters to the MessageBox function.
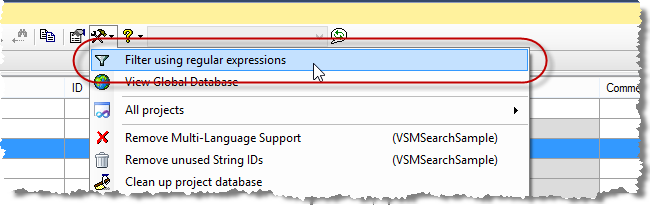
You can handle operations like this easily with the feature "Filter with regular expressions". You can select this option from the tools menu as shown below, or from the context menu in the source code grid.
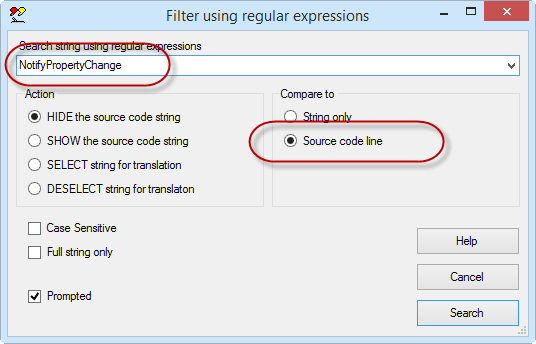
This command shows the filter dialog, in which you can enter a search string as a regular expression. For example in the screenshot shown below, the search string "^select " will search for any string starting with the word select, with the option to hide the string.
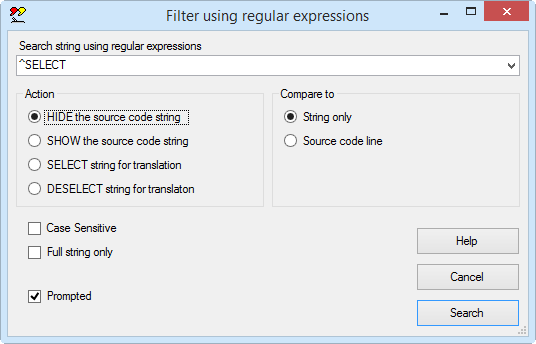
The dialog offers the option to match only the string, or the complete source code line. By matching the complete code line, it is easy to detect strings used in particular function calls.
For example, we can find all calls to the function NotifyPropertyChanged and hide them.
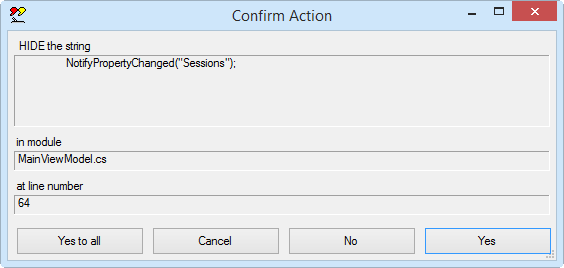
When the string is found, the Add-In asks whether the specific string should actually be hidden.
Using the translation memory
Aside from the project database used to store the translations for an individual project, the Multi-Language Add-In also stores all translations in global translations database. When it detects an exact match between a new text and a translation stored in the global database, it will insert the translation automatically. This is great for common terms like OK and Cancel.
If you are able to translate the texts yourself, then the translation memory provides an additional help, based on the translations stored in the global database. To use the translation memory, first click in the cell you want to edit, and then hit F3 or F12. The following screenshot shows the translation memory dialog with the text Add a new language to the project, which should be translated into German.
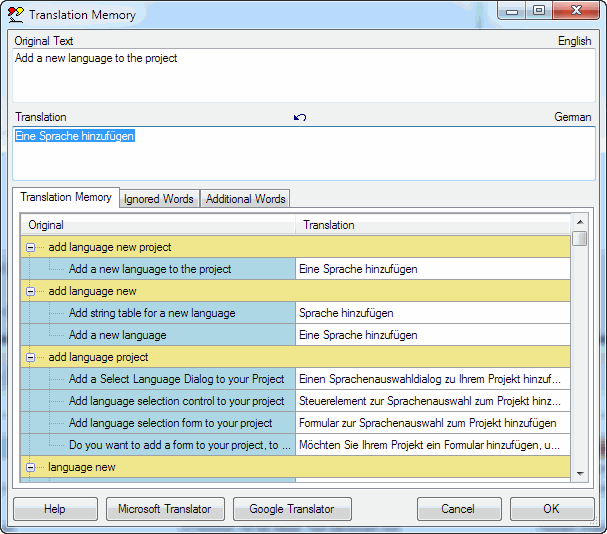
In the lower part of the dialog, there is list of existing translations, containing one or more of the same words as the string to be translated. The list is sorted according to the number of matching words, so the most useful translations should be near the top. You can copy words out of the grid and edit the new translation in the edit box marked Translation.
Obviously, the common words "a", "to" and "the" will not be of much help. If you select the tab Ignored words, you can select the words which are to be ignored. The Add-In keeps a list of ignored words in the global database and automatically ignores these words in future.
The translation memory feature is particularly useful for technical terms where you might not be familiar with the correct translation and where you want to use terms consistently.
Using the Spreadsheet export
If you are not able to translate the texts yourself, you will have to give them to a translator. For this purpose you can use the Spreadsheet export/import feature. There are two versions of this feature:
- the simple version with one worksheet and no macros (for Excel or OpenOffice)
- the three worksheet structured export with macro support (for Excel)
Both versions are accessed via the Excel symbol  on the toolbar.
on the toolbar.
The screenshot below shows the format of the simple spreadsheet file. As you can see, the first column contains the string ID number, followed by a column for each language. The first two rows contain the language names and the locale ID numbers.
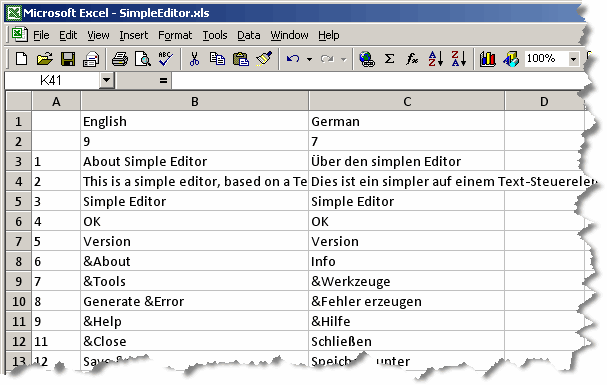
The translator should update texts in the appropriate language column, without changing the format of the file. When the translator is complete, you can import the translations back into the project.
The three worksheet format contains two additional worksheets, which closely resemble the controls grid and the source code grid in the Add-In. These worksheets provide more context information for the translator. Because all texts in the additional worksheets are also present in the third worksheet, Excel macros are used to maintain consistency within the file. The macros also provide some additional functionality, similar to some of the functions provided by the Add-In.
The three worksheet is to be recommended, unless your organization is adamantly opposed to using macros.
Exporting the texts to resource files
|
The Multi-Language Add-In automatically generates resource strings for the texts in your project. For Windows Store projects, the resource strings are stored in resource files with the extension .resw in a standardized directory structure. At the top level there is a directory named Strings. Within this directory, there are separate directories for each language, named with the standard language and region codes. In each language directory there is a file named Resources.resw. The "Build Action" for this file is set to PRIResource. |

|
You do not have to worry about any of these details. The files are generated by the Add-In.
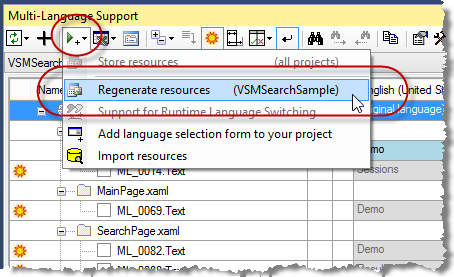
|
If you have any doubt that the resources have been generated correctly, then you can regenerate them at any time with the command Regenerate resources in the drop down menu shown here. |
Selecting the language of the application
It is very practical to be able to select the language for your application, independently of the language used by Windows. This is almost essential for testing, but you may also want to make it a permanent feature of your application. We must consider two cases separately:
- selecting the language when the program starts
- changing the language of the running program
It is fairly straightforward to change the language of Windows Store application with the following steps (in C#):
// Override for the app's preferred language ApplicationLanguages.PrimaryLanguageOverride = ci.Name ; // Reset the resource manager ResourceManager.Current.DefaultContext.Reset(); // Reload the page if ( Frame != null ) Frame.Navigate ( typeof ( MainPage ) ) ;

|
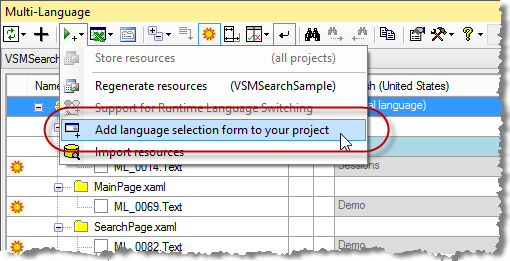
The Multi-Language Add-In can add a page to your project which appears when you start the project, which allows the user to select the language of the application. |
To add this feature, click on the runtime support symbol  on the toolbar and select the command Add language selection form to your project from the dropdown menu.
on the toolbar and select the command Add language selection form to your project from the dropdown menu. |
|

|
This brings up a dialog showing which actions are necessary to add the language selection page to your project. Click on Add Now to start the operation. This will add a page called SelectLanguage to your project and modify the code in the OnLaunched method in App class to show page. |
rootFrame.Navigate(typeof(MainPage), e.Arguments);
MultiLang.SelectLanguageParameters sl = new MultiLang.SelectLanguageParameters
{ MainPageType = typeof(MainPage), Arguments = e.Arguments } ;
rootFrame.Navigate(typeof(MultiLang.SelectLanguage), sl);
The first line creates a new object to store the type of the first page and the parameters which are passed to that page. The second line shows the language selection page and passes this object into the page as an argument.
When you select the language and click on "Continue" the language selection page sets the language and then starts the original first page, with its original parameters.